一、什么是坐標(biāo)系？

三次元測(cè)量?jī)x又稱三坐標(biāo)，常常需要建立坐標(biāo)系，那么什么是坐標(biāo)系呢？思瑞測(cè)量三坐標(biāo)服務(wù)工程師告訴你答案：這是理科常用輔助方法。常見有直線坐標(biāo)系，平面直角坐標(biāo)系。為了說明質(zhì)點(diǎn)的位置、運(yùn)動(dòng)的快慢、方向等，須選取其坐標(biāo)系。在參照系中，為確定空間一點(diǎn)的位置，按規(guī)定方法選取的有次序的一組數(shù)據(jù)，這就叫做“坐標(biāo)”。在某一問題中規(guī)定坐標(biāo)的方法，就是該問題所用的坐標(biāo)系。

二、坐標(biāo)系的種類

坐標(biāo)系的種類很多，常用的坐標(biāo)系有：笛卡爾直角坐標(biāo)系、平面極坐標(biāo)系、柱面坐標(biāo)系（或稱柱坐標(biāo)系）和球面坐標(biāo)系(或稱球坐標(biāo)系)等。中學(xué)物理學(xué)中常用的坐標(biāo)系，為直角坐標(biāo)系，或稱為正交坐標(biāo)系。

三、平面極坐標(biāo)系

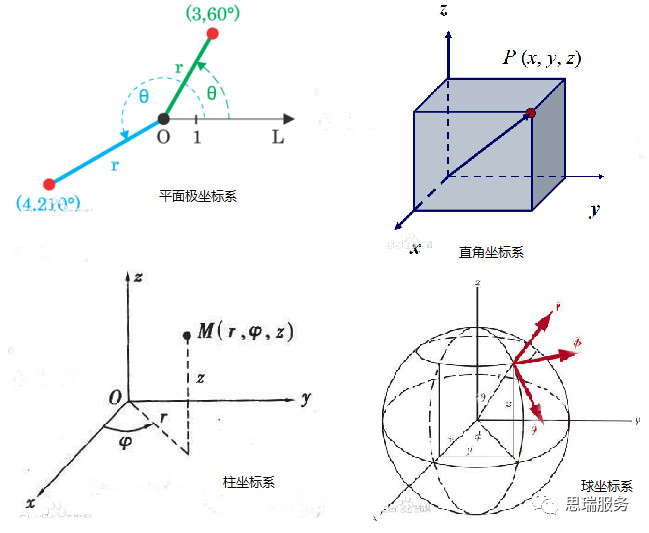
我們平常講的二維極坐標(biāo)系就是平面極坐標(biāo)，而我們?cè)谌卧獪y(cè)量?jī)x中的極坐標(biāo)則是在平面極坐標(biāo)系的基礎(chǔ)上加了Z軸，也就是上圖中的柱坐標(biāo)。下面我們先來學(xué)習(xí)一下平面極坐標(biāo)。

如圖所示，在平面上取一定點(diǎn)O，稱為極點(diǎn)，由O出發(fā)的一條射線OX，稱為極軸。再取定一個(gè)長(zhǎng)度單位，通常規(guī)定角度取逆時(shí)針方向?yàn)檎＿@樣，平面上任一點(diǎn)P的位置就可以用線段OP的長(zhǎng)度 R以及從OX到OP的角度 A來確定，有序數(shù)對(duì)（R，A）就稱為P點(diǎn)的極坐標(biāo)，記為P（ R，A )；R稱為P點(diǎn)的極徑，A稱為P點(diǎn)的極角。P點(diǎn)坐標(biāo)為（2，60°）

四、柱坐標(biāo)系（三次元測(cè)量?jī)x中使用的極坐標(biāo)）

        柱坐標(biāo)系其實(shí)就是平面極坐標(biāo)系的基礎(chǔ)上加上Z軸（H軸）形成的三維坐標(biāo)系，那么柱坐標(biāo)系和直角坐標(biāo)系之間是如何轉(zhuǎn)換的呢？

下面我們來看一個(gè)例子:

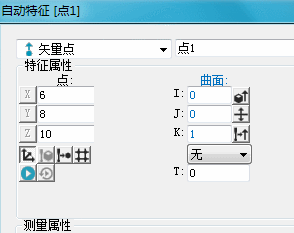
如圖所示：在直角坐標(biāo)系中點(diǎn)M（6，8，10），那么如何用極坐標(biāo)表達(dá)這個(gè)點(diǎn)？

知識(shí)點(diǎn)

直角坐標(biāo)系（x，y，z）與ρ-XY柱坐標(biāo)系(R,A,H)的轉(zhuǎn)換關(guān)系：

當(dāng)柱坐標(biāo)系以直角坐標(biāo)系Z軸為H軸時(shí)：

即柱坐標(biāo)系ρ-XY中，R=√(6^2+8^2 )=10，

A=tan^-1(8/6)=53.13 ，H=Z=10

M的坐標(biāo)為（10，53.13°，10）

依次類推，當(dāng)柱坐標(biāo)系以直角坐標(biāo)系Y軸為H軸時(shí)，

即坐標(biāo)系為ρ-XZ中，R=√(6^2+10^2 )=11.662，

A=tan^-1(-8/6)=120.964°，H=Y=8

M坐標(biāo)為（11.662，120.964°，8）

當(dāng)柱坐標(biāo)系以直角坐標(biāo)系X軸為H軸時(shí)：

即坐標(biāo)系為ρ-YZ中，R=√(8^2+10^2 )=12.806，

A=tan^-1(10/8)=51.34° ，H=X=6

M點(diǎn)坐標(biāo)為（12.806，51.34°，6）

關(guān)于三坐標(biāo)極坐標(biāo)系的知識(shí)我們就講到這里，你是否明白了呢？下期我們來講極坐標(biāo)在日常測(cè)量中的運(yùn)用，盡情期待!