400-8800-268
對(duì)于熟悉PC軟件的人來(lái)說(shuō)IJK并不陌生,測(cè)點(diǎn)的矢量、自動(dòng)特征的曲面矢量、棱矢量等都會(huì)用到IJK,但是IJK的應(yīng)用是否準(zhǔn)確,對(duì)于測(cè)量都有哪些影響呢?我想很多使用人員并不盡然全都知道。下面我來(lái)總結(jié)幾點(diǎn)日常使用中遇到的一些情況。
一、測(cè)頭校驗(yàn)
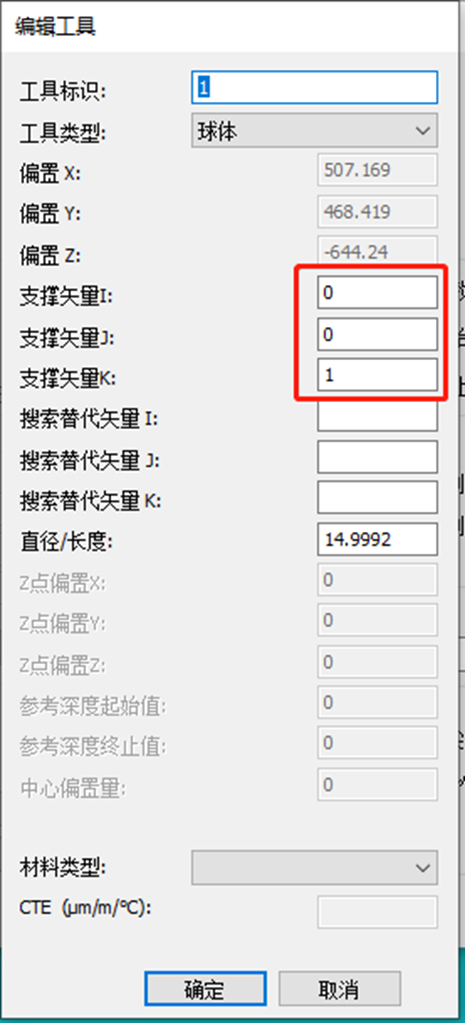
在測(cè)頭校驗(yàn)時(shí),可用工具列表中需要設(shè)置標(biāo)準(zhǔn)球的支撐矢量。對(duì)于常規(guī)垂直向上的標(biāo)準(zhǔn)球,IJK則分別要設(shè)置成001。當(dāng)用到星型針時(shí),有時(shí)需要把標(biāo)準(zhǔn)球裝到側(cè)邊(多方向底座),幾個(gè)不同方向?qū)?yīng)的IJK分別是:X+ 1、0、0;Y+ 0、1、0;X+ -1、0、0;Y- 0、-1、0。
二、矢量點(diǎn)
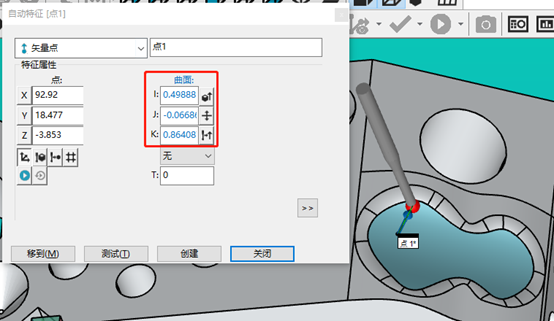
我們知道手動(dòng)測(cè)量點(diǎn)的補(bǔ)償是單軸補(bǔ)償?shù)摹1热缯f(shuō),測(cè)針往Z-方向打點(diǎn),最終點(diǎn)的坐標(biāo)值是通過(guò)獲取紅寶石中心的坐標(biāo)再加上測(cè)針的補(bǔ)償半徑,從而得到準(zhǔn)確的Z坐標(biāo)。如果測(cè)針斜著打點(diǎn),就會(huì)根據(jù)測(cè)針的反彈反向與哪個(gè)坐標(biāo)軸的夾角最小,則會(huì)沿著該坐標(biāo)軸進(jìn)行半徑的補(bǔ)償。所以我們?cè)跍y(cè)斜面和曲面時(shí),則要求導(dǎo)入數(shù)模,通過(guò)軟件的自動(dòng)矢量點(diǎn)獲取模型的理論矢量,從而在測(cè)量時(shí)根據(jù)該矢量(IJK)進(jìn)行三軸的同時(shí)補(bǔ)償。雖然該補(bǔ)償方式不是最完美的,但也是目前最合適的補(bǔ)償方式。
三、自動(dòng)圓及同心度
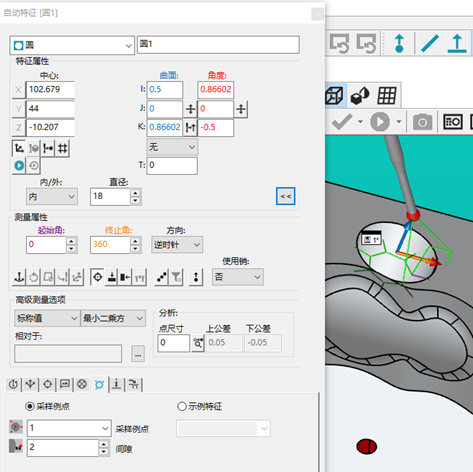
自動(dòng)圓中有個(gè)曲面矢量的設(shè)置,一般情況我們會(huì)根據(jù)投影方向設(shè)置對(duì)應(yīng)的IJK或者通過(guò)模型直接抓取。對(duì)于很多使用人員測(cè)量圓會(huì)設(shè)置樣例點(diǎn)(一般樣例點(diǎn)的設(shè)置≥3個(gè)),這樣一來(lái)圓的理論IJK就會(huì)根據(jù)樣例點(diǎn)形成的平面矢量發(fā)生變化。在同心度評(píng)價(jià)時(shí),同心度是投影到基準(zhǔn)圓的理論IJK計(jì)算的,所以有時(shí)候發(fā)現(xiàn)通過(guò)量?jī)蓤A圓心距數(shù)據(jù)很好,但同心度很差。因?yàn)檫@個(gè)時(shí)候計(jì)算同心度已經(jīng)按照基準(zhǔn)圓那幾個(gè)樣例點(diǎn)形成的小平面進(jìn)行投影的計(jì)算了,對(duì)于兩個(gè)圓距離越遠(yuǎn)越明顯。對(duì)于這種情況,我們可以通過(guò)設(shè)置1個(gè)樣例點(diǎn),即保證了能測(cè)到圓,又不改變圓的理論IJK。
自動(dòng)圓中有個(gè)曲面矢量的設(shè)置,一般情況我們會(huì)根據(jù)投影方
對(duì)于斜面上兩個(gè)孔測(cè)同心度,建議先用斜面(面盡量取大一點(diǎn))進(jìn)行找正,盡量不要直接在模型上抓取兩個(gè)理論圓進(jìn)行測(cè)量并評(píng)價(jià)。如果面很小,則考慮是否可以通同軸度或者用長(zhǎng)圓柱作為基準(zhǔn)。
四、手動(dòng)圓柱的位置度
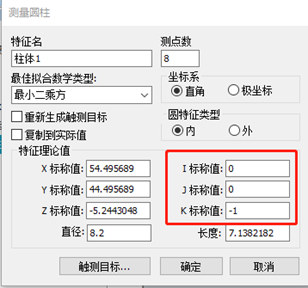
在評(píng)價(jià)圓柱的位置度時(shí),特別手動(dòng)圓柱,經(jīng)常會(huì)發(fā)現(xiàn)報(bào)告出來(lái)的理論值和輸入的不一樣。那是因?yàn)闆](méi)有對(duì)手動(dòng)圓柱的理論IJK進(jìn)行修改。如果不改理論IJK,軟件就會(huì)以第一次編程時(shí)的IJK作為理論值,最差點(diǎn)(起始點(diǎn)或終止點(diǎn))理論坐標(biāo)值則用偏離該IJK多少計(jì)算而得。所以在測(cè)手動(dòng)圓柱位置度時(shí)一定要修改理論IJK,或者用自動(dòng)圓柱。
 返回頂部
返回頂部